事物之间的关系可以分为：

1. 无关系
2. 一对一
3. 一对多
4. 多对多

因此，从这个角度逻辑结构分为：

1. 集合结构 （无关系）
2. 线型结构 （一对一）
3. 树型结构 （一对多）
4. 图型结构 （多对多）

物理结构指计算机为了体现逻辑结构，物理上存储数据的方式。

物理结构分为：

1. 顺序存储
2. 链式存储

使用一段连续的存储空间来对数据进行存储。

可以使用任意的存储空间对数据进行存储，但是会 存储额外的信息来体现他们之间的关系 。

使用连续或连续的空间，保存数据本身，再使用额外的空间保存地址（用来维护相互间的关系）

每个节点由两部分构成

1. 存储数据的数据域
2. 存储后继节点的地址域

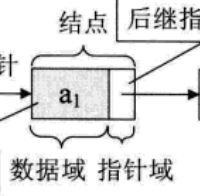
/* 单链表存储结构 */
typedef struct LNode{
    ElemType   data;
    struct LNode  *next;
}LNode, *LinkList;

对链表的操作主要包括两部分，

1. 查询到指定节点
2. 插入或删除节点

查询节点的性能为O(n), 而插入或删除为O(1).

指向线性表中第一个节点的指针即为头指针。

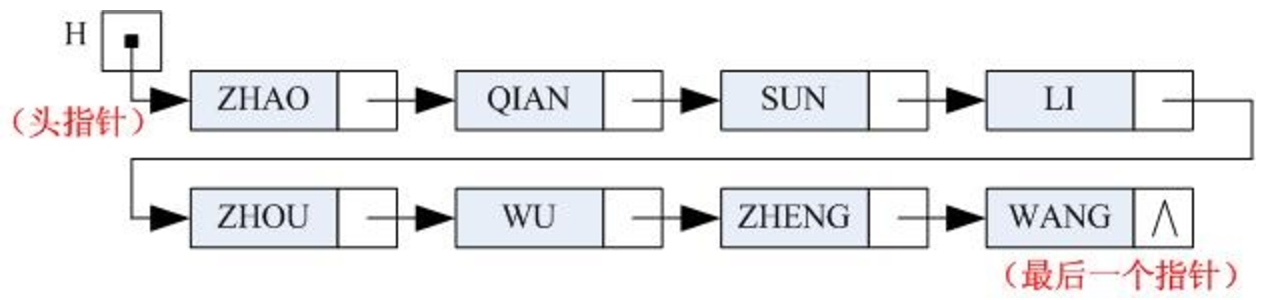
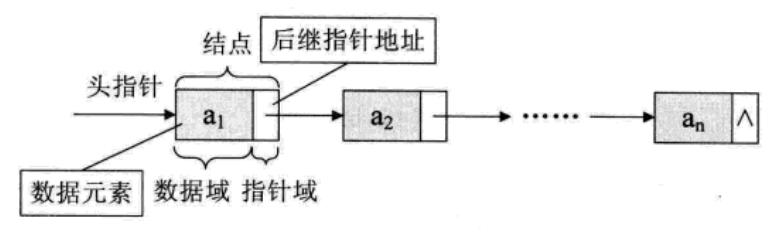
• 在线性表的链式存储结构中，头指针是指链表指向第一个结点的指针，若链表有头结点，则头指针就是指向链表头结点的指针。
• 头指针具有标识作用，故常用头指针冠以链表的名字。
• 无论链表是否为空，头指针均不为空。头指针是链表的必要元素。

出于统一操作逻辑，优化算法的目的，会在单链表的第一个结点（有效元素）之前附设一个结点，称之为头结点

• 头结点是为了操作的统一与方便而设立的，放在第一个元素结点之前，其数据域一般无意义（当然有些情况下也可存放链表的长度、用做监视哨等等）。
• 有了头结点后，对在第一个元素结点前插入结点和删除第一个结点，其操作与对其它结点的操作统一了。
• 首元结点也就是第一个元素的结点，它是头结点后边的第一个结点。
• 头结点不是链表所必需的。